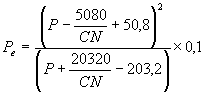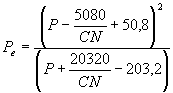Caudais máximos

O calculo dos caudais máximos que poderão ser atingidos em certas situações pré- definidas é efectuado com um fim de planeamento e possível prevenção, variando assim a sua precisão de acordo com o seu fim.

Estes caudais podem ser obtidos através de vários métodos entre os quais as formulas empíricas, formulas cinemáticas e o método do hidrograma unitário.

 

Fórmula racional

Esta formula apenas deve ser utilizada para bacias pequenas como é o caso(<= 25km²).

em que :

Qmáx. - Caudal máximo de cheia em m³/s

C- Coeficiente de escoamento adimensional (ver anexo)

i- Intensidade da chuva em m/s

A- Área da bacia em m²

A = 5,823 Km² = 5,823

C=0,3

t = 1,08 h = 65 min (Este valor de t , corresponde ao Tc da formula de Kirpich)

para:

Tr = 5 anos - I = 259,26 * t -0,562

Tr = 10 anos - I = 290,68 * t -0,549

Tr = 100 anos - I = 365,62 * t -0,508

Logo:

Tr

(anos)

I

(mm/h)

I

(m/s)

Qmáx

(m3/s)

5 24,824 6,896x10-06 12,046
10 33,630 9,342x10-06 16,319
100 43,860 1,218x10-05 21,283

Fórmula de Loureiro

Em que :

Qp- Caudal de ponta de cheia em m³/l

Z - Parâmetro regional

A - Área da bacia em Km²

C - Parâmetro relacionado com o tempo de retorno (Tr)

Z= 0,784

Para :

Tr = 5 anos - C = 3,45

Tr = 10 anos - C = 4,40

Tr = 100 anos - C = 7,09

Logo :

Tr

(anos )

Qp

(m³/s)
5 13,731
10 17,512
100 28,218

Fórmula de Giandotti

Em que:

Qmáx - caudal máximo em m³ /s

l - parâmetro tabelado (depende da área )

A - área em Km²

h - altura da precipitação máxima em mm ( depende de Tc e de Tr )

Tc - tempo de concentração em horas

Tc(Giandotti) = 2,12h

l = 0,346

A = 5,823 km2

L = 5,911 Km

Para:

Tr = 5 anos

Tr = 10 anos

Tr = 100 anos

Então:

Tr

(anos)

h

(mm)

Qmáx

(m³/s)
5 36,133 34,340
10 43,084 40,945
100 66,141 62,858

Fórmula de Mockus

Para o tempo de chuva efectiva estabelece-se um tempo crítico

sendo Tc o tempo de concentração.

Tc=1,08h=65min

O tempo de chuva será


onde Ia são as perdas iniciais (valor médio) obtido pela fórmula

sendo CN o número de escoamento ou curva número (CN=86,70).

Tr=5 anos

Tr=10 anos

Tr=100 anos

I(Tcr) é a intensidade da chuva, correspondente ao tempo crítico Tcr e obtém-se a partir da respectiva equação de chuvas com I em mm/h e Tcr em horas.

A altura P calcula-se recorrendo à equação de chuvas do Algarve

Tr=5 anos

Tr=10 anos

Tr=100 anos

A chuva efectiva calcula-se através da fórmula do SCS:

P em mm

Pe em cm.

O caudal máximo foi calculado pela fórmula:

Qmáx em m3/s

Tc em horas

A tabela seguinte resume os cálculos efectuados:

Tr

(anos)

t

(horas)

P

(mm)

Pe

(cm)

Qmáx

(m3/s)

5 0,653 26,890 0,628 4,509
10 0,551 31,780 0,914 6,561
100 0,369 47,460 2,001 14,365

Hidrograma Unitário Triangular

em que :

Qp - caudal em m³/s

A - área da bacia em Km²

Tp - tempo de ascensão em horas

em que:

D - tempo unitário

Tc - tempo de concentração em horas(Kirpich)

TC=1,08h

Tempo unitário :

Tempo de precipitação:

Tempo de retorno:

Assim

A = 5,823 km²

Tc = 1,08 h

Caudal pique:

Para o cálculo do Hidrograma Unitário Triangular:

Precipitação efectiva:

Volume escoado:

Hidrograma Unitário Triangular

Tabelas e Hidrogramas Unitários

Depois de uma análise das Tabelas referentes ao Hidrograma Unitário Triangular, obtivemos os seguintes caudais máximos:

Tr=5 anos

Tr=10 anos

Tr=100 anos